有機合成の収率や純度はバラつくものだからしょうがない、と諦めがちですが、工業化のうえではバラツキは天敵です。
コスト、安定供給、安定品質は商売するうえで外せないものだからです。
ICH-Q11 にて統計的手法を取り入れることが推奨されたこともあり、医薬品開発においても統計学は盛んに取り入れられてきています。
今回はその一例を示した論文から、分散分析による条件検討方法を紹介したいと思います。
Quality by Design in Action 1: Controlling Critical Quality Attributes of an Active Pharmaceutical Ingredient
Abdul Qayum Mohammed†‡, Phani Kiran Sunkari†, P. Srinivas*‡ and Amrendra Kumar Roy*†
Organic Process Research & Development
Vol. 19: , Issue. 11, : Pages. 1634-1644
Publication Date (Web): January 21, 2015
実際に行った実験結果ではなく、QbD(Quality by Design)に基づくプロセス検討のモデルケースを示した論文です。
様々な方法論が述べられていますが、今回はANOVA(分散分析)にスポットを当てて紹介します。
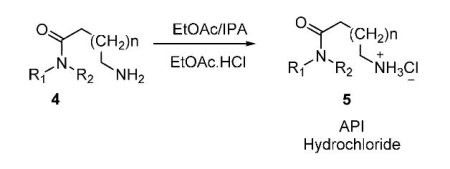
さて、題材となる工程は以下の通りです。
1級アミンを塩酸塩にする工程ですね。
API(Active Pharmaceutical Ingredient : 原薬)の最終工程ではよく見られます。
反応工程ほど複雑ではないですが、最終工程での収率ダウンはコストに響きますし、不純物生成は品質低下を招きます。
たかが造塩工程と侮るなかれ、です。
著者らは本工程で重要なパラメータを3つピックアップしました。
(これらのパラメータを、実感計画法では「因子」と呼びます。以降も因子で統一します。)
1) IPA溶媒量
2) 塩酸投入時の温度
3) 塩酸の当量
続いてこれら3因子について、各々2つの条件(2水準、と呼びます。)を設定し、2×2×2=8実験を総当たりで行います。
このように、考えうる条件を総当たりで行う方法を完全実施要因計画 Full Factorial Designと呼びます。
メリットは各因子の交互作用(後述します)を全て検証できることですが、実験数が多くなることがデメリットです。
実験数を減らすことを重視する場合は、一部実施要因計画が適しています
これでようやく実験開始!と思いきや、あと一手間が必要です。
各3因子について、先程設定した2水準の中間となる値(=最適値と予想される値)で実験します。
しかも、同じ条件を4回!
何のためかと言うと、「普通に実験した時の誤差」を求めるためです。
同条件で実験しても収率や純度はバラツキますよね、そのバラツキの程度を求めます。
先に勘所を言ってしまいますが、「普通に実験した時の誤差」と「パラメータを変更して実感した時の誤差」を比較して、後者の方が明らかに誤差が大きい場合には、そのパラメータは結果へ有意に影響しているとみなす、というのが分散分析の仕組みです。
Advertisements
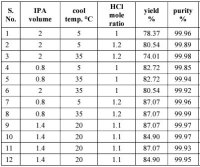
ここまでをまとめますと、合計12実験を上記の表の通りの条件で行うことになります。
プロトコルに関する話はここまで。以降は結果の解析方法についてです。
不純物生成への影響はないという結果なので、これも割愛。収率への影響に話を絞ります。
ざっと見ると、IPA溶媒量を減らした方が良い結果になっているようです。
1つ1つの条件を比較していくと、塩酸当量が多い方が良いことも気付けるかと思います。
分散分析によって得られる情報もおおよそ上記と一致していますが、さらにもう一つ「IPA溶媒量と塩酸当量の交互作用」についても収率に影響するという結果が得られています。
因子同士が互いに影響し、相乗効果が得られる場合に「交互作用がある」と呼びます。
1+1=3になる時もありますが、逆に1+1=0.5になってしまう時もあるので注意しなければなりません。
1つずつパラメータを検討していく(一因子実験)では、交互作用にはなかなか気づくことができません。
なぜ一因子実験では分からないことが分散分析で確認できるのか、結果をさらに詳しく見ていきましょう。
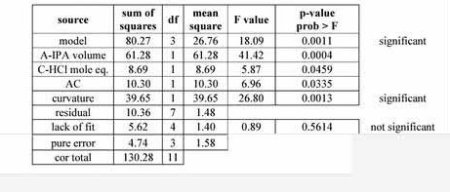
まずは用語解説とともに、表を説明していきます。
sum of squares :平方和。実測値と平均値の差を二乗した値。
df :自由度。
mean squares :平均平方。平方和を自由度で割った値。実験数が増えるほど平方和は大きな値になるので、自由度で割ることで一律に比較できるようになる。
F value :F値。residual(残差)の平均平方を1とした時、対象の平均平方が何倍に相当するかを示す。
p-value :p値。有意確立。F値、F値の分子の自由度、F値の分母の自由度によって求められる(excelならF.DIST.RT関数)。
今回の場合、「モデル曲線は的外れで、実験値は偶然バラついた結果と仮定した場合(本当に主張したいことを、あえて否定します。帰無仮説と呼びます。)、得られたF値以上になる確率」を示しています。p値が0.0004ということは、全くの偶然で起きる確率は0.04%ということ。そんな奇跡が起きたと考えるよりは、帰無仮説が間違っていると考えましょうよ、という論理です。
curvature : 曲率。低水準と高水準の間に変曲点(極大値または極小値)が存在することを示す。最適解を求めるために分散分析では線形近似を行うが、変曲点がある場合には上手くフィッティングしない。この場合、応答局面法(RSM)等を用いる必要がある。
lack of fit : 不適合度。モデル式がフィッティングしているかをあらわす。
pure error : 純粋誤差。原因を特定できない、偶然によって起きる誤差。
cor total : (実測値 - 全実測値の平均値)^2 の総和。この値をmodel、curvature 、residualに分けることが出来る。
modelの平均平方(IPA溶媒量、塩酸当量、それらの交互作用、によってもたらされた平均値からのズレ)が、residualの平均平方(どの実験でも平等に起きうる、原因が説明できない平均値からのズレ)に対して非常に大きいことから、「ただの誤差で起きるバラツキとは到底考えられない。IPA、塩酸が収率に影響していると考えるべき!」という結論に結びつきます。
ようやく結論に辿り着きました、めでたしめでたし。
今回紹介した例は、再現性の良い(ロバストである)こと、誤差が出にくい条件にすること、を目的とした実験でした。医薬品の工業的プロセスを確立するうえで、とても重要な方法論といえます。
一方、反応結果をシミュレートするモデルを方程式であらわすことができるので、これを利用して最も収率が高くなる、または最も純度が良い条件を導くことができます。アカデミック分野の方にはこのメリットが有用かもしれませんね。