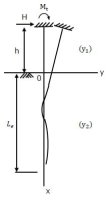
一般に長い杭の条件は、β・Lp≧2.5~πとかβ・Lp≧2.25とか言われています。
ここでは、Changの式から長い杭をどう判断すると良いかを考えてみます。
杭頭回転拘束(杭頭固定)におけるChangの式は、
変位 :X(y) = e-βy(cosβy+sinβy)・Hp/(4β3EI )
曲げモーメント:M(y) = -e-βy( sinβy - cosβy )・Hp/(2β )
せん断力 :Q(y) = -HP・e-βycosβy
ここに、Hp :杭頭水平力(kN),y:深度(m)
長い杭の必要条件は、杭の変位X(L)=0となる深度Lまで杭が挿入されていることです。
e-βy>0であることからX(y)=0となるのは、cosβL+sinβL=0となる場合となります。
sinβL/cosβL=-1
tanβL=-1
したがって、βL=3/4π、7/4π・・・(=(n-1/4)・π)) n=1,2,3,・・・
最初にcosβL+sinβL=0となる3/4πに着目すると、
βL=3/4π=2.356
以上です。
いろいろと条件(数値)を設定して、Changの式で計算してみました。(つづきます)
半無限長の杭となる杭長を、Changの式で杭の曲げモーメント、せん断力、変位量を求めて確認してみました。
地盤の変形係数はN値から求めました。E0=700N(kN/m2)。N値は5の粘性土を想定しています。
杭はコンクリート杭(中実)で、杭径D=1.00(m)、ヤング率E=2.26×10^7(kN/m2)、断面2次モーメントはI=4.91×10^-2(m4)としました。
β=0.211(1/m)となったので、1/β=4.731(m)となりました。
断面力計算結果は次のとおり。
グラフにしてみると分かりますが、βL=2.5では曲げモーメント、せん断力が杭に作用しています。安全側の設計をするのであれば、βL=πとした方が良さそうです。