Advertisements

地盤の基本固有周期は、主に以下の式から算出されます。

平均せん断弾性波速度V_Siは、弾性波探査やPS検層等で直接計測して求める場合が望ましいですが、N値による推定式がよく適用されます。道路橋示方書に準拠した設計では、以下の式が使われます。 

・粘性土層の場合

V_S＝100×N_i^1/3（1≦N_i≦25）

・砂質土層の場合

V_S＝80×N_i^1/3（1≦N_i≦50）

Ni：標準貫入試験によるi番目の平均N値

道路橋示方書では、せん断波速度が300m/s以上の地盤を堅固な地盤（耐震設計上の基盤）であると見なしていますので、この式の適用上限はV_S=300m/sと考えられます。そのためN値の上限は、粘性土は25、砂質土は50としています。

なお、N値がゼロの場合はV_S=0m/sとなってしまうので、V_S＝50m/sとするとされています。後で述べますが、今井･殿内の提案式では沖積粘性土層では定数項を80としていますので、N値がゼロの場合にV_S＝50m/sとするのは、ややT_Gを大きく評価することになりますが概ね妥当であると考えます。

この文章では、まず、N値からVsを算定する式のうち、よく使われるものを比較し、その後に地盤の基本固有周期がT_G＝4Σ(H_i/V_Si)となる理由についての説明を行うことにします。

(1)N値によるVsの推定式比較

N値からせん断弾性波速度（S波速度）を求める推定式が複数提案されています。一般に用いられる推定式を以下に示します。

a)今井の式および派生式

V_S=89.8･N^0.341　　　　　　　　 ・・・今井の式(1)

V_S=97.0･N^0.314　　　　　　　　 ・・・今井の式(2)

V_S=80･N^1/3（砂質土）(1≦N≦50)・・・道路橋の式

V_s=100･N^1/3（粘性土）(1≦N≦25)・・・道路橋の式

V_s=a･N^b+c　　　　　　　　　　 ・・・今井･殿内の提案式(修正式)

b)建築設計にてよく使われる式

V_S=69･N^0.171･(H/H₀)^0.2･Y_g･S_t　　 ・・・太田・後藤の提案式(修正式)

ここに、

V_S：せん断波速度=S 波速度（m/s）

N：層の平均Ｎ値

H：地表面から層の中心までの深度（m）

H₀：基準深度（=1.0m）

Advertisements

Y_g：地質年代係数（沖積層1.0、洪積層1.3）

S_t：土質に応じた係数（粘性土1.0、砂質土･砂礫土1.1、礫質土1.4）

前者5式は今井の式そのものまたは派生式です。今井の式の派生式のうち、今井・殿内修正式は沖積層と洪積層で係数を変えることが特徴的です。最後の太田・後藤の提案式(修正式)は地層深さと地質年代がパラメータとなっています。

1)粘性土

図‐1は粘性土の場合のN値—V_S関係です。

クラフの勾配に着目すると、太田・後藤修正式の勾配は小さく、道路橋式と今井式及び今井・殿内修正式は勾配が大きい傾向にあります。その結果、道路橋式と今井式及び今井・殿内修正式は、太田・後藤修正式を横切るような様子となっています。

道路橋式において適用上限がN値≦25となっているのは、N値＞25では、算出されるV_Sが、太田・後藤修正式の沖積粘性土層のH=40mの場合より大きくなり、過大な結果を与えるからではないか？ということも理由にあると推測できます。

一方、太田・後藤修正式に着目すると、同じN値であっても、深度が深い方が、また沖積層より洪積層の方がV_Sが大きくなります。前者は、式中の(H/H₀)^0.2によるもので、側方土圧による拘束力の影響を考慮しています。後者は式中のY_gによるもので、固結等の年代効果を考慮しています。

道路橋式は、層の深さや年代効果を考慮していないことから、使用する際には注意を要します。 

2)砂質土

図‐2は砂質土の場合のN値—V_S関係です。グラフに描かれる曲線の傾向は、粘性土の場合と同様です。

クラフの勾配に着目すると、太田・後藤修正式の勾配は小さく、道路橋式と今井式及び今井・殿内修正式は勾配が大きい傾向にあります。その結果、道路橋式と今井式及び今井・殿内修正式は、太田・後藤修正式を横切るような様子となっています。

道路橋式において適用上限がN値≦50となっているのは、N値＞50では、算出されるV_Sが、太田・後藤修正式の沖積砂質土層のH=40mや洪積砂質土層のH=20mの場合とほぼ同じとなり、N値の測定精度も相まって過大な結果を与えるからではないか？ということも理由にあると推測できます。土木の世界では標準貫入試験の測定上限が50とされています。一方、建築の世界では60とすることが多いのは、この辺りの経緯と関連していると思われます。

一方、太田・後藤修正式に着目すると、同じN値であっても、深度が深い方が、また沖積層より洪積層の方がV_Sが大きくなります。前者は、式中の(H/H₀)^0.2によるもので、側方土圧による拘束力の影響を考慮しています。後者は式中のY_gによるもので、固結等の年代効果を考慮しています。

道路橋式は、層の深さや年代効果を考慮していないことから、使用する際には注意を要します。 

3)礫質土

図‐3は礫質土の場合のN値—Vs関係です。道路橋式と今井式及び今井・殿内修正式（沖積層礫質土）は、N値が10以下ではVsがかなり小さくなります。ただし、道路橋式は砂質土用の式です。

沖積層礫質土では、今井・殿内修正式は、太田・後藤修正式を横切るような様子となっていますが、N値が10～40の間では太田・後藤修正式（沖積層礫質土）のH=5～20mの間にいます。これは洪積層礫質土でも同様で、N値が10～100の間では、今井・殿内修正式のVsは、太田・後藤修正式のH=5～20mの間にいます。

砂質土用の道路橋式を礫質土に適用すると過小な結果となる可能性があることに留意する必要があります。

(2) 地盤の基本固有周期がTG＝4Σ(Hi/Vsi)となる理由

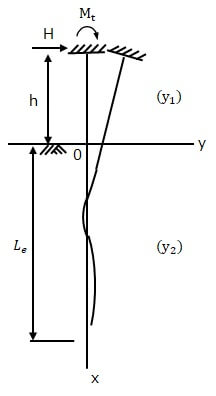
説明を簡単にするため、図-4に示す地下地盤を最も単純な基盤層の上に表層地盤が1層のみ存在する2層モデルを考えます。

重複反射理論では、表層地盤の増幅特性は式1で表されます。

なお、地表面（露頭面）では、上層がない（もしくは無視する）ため、α＝0.0となり全反射します。したがって、上昇波＝下降波となって伝播するため、地表面での地震波は上昇波の2倍（2Eと呼ばれる）として評価されます。 

基盤の密度ρとせん断波速度V_Sは、表層地盤よりも大きいことから次のような関係となるため、

0＜ρ₂･V_S2≦ρ₁･V_S1

波動インピーダンス比αの範囲は、0＜α≦1となります(実地盤では、下層より上層の地盤の方がせん断波速度が大きいこともあり、ρ₂･V_S2＞ρ₁･V_S1という状況もあり得ます)。

波動インピーダンス比αを0～1まで変化させて式1のグラフを描いてみました(図-5参照)。αが小さくなると応答振幅比(増幅率)が大きくなることが分かります。つまり、表層の密度が小さいほど、またせん断波速度が小さいほど応答振幅が大きくなります。

また、地表での応答振幅比は、ωH/Vs₂=(2n-1)・π/2の時に最大値を示します。

入射波の周期をTとするとω･T=2πとなります。図-5よりωH/V_S2=(2n-1)･π/2で大きな増幅となることから、地盤の揺れが1次モードの場合、T₁=4H/Vs₂がこの表層地盤の１次の卓越周期となります。これが地盤の基本固有周期と呼ばれるものです。同様にT₂=4/3・H/V_S2が2次の卓越周期、T₃=4/5・H/V_S2が3次の卓越周期となります(図-6参照)。

なお、１次の卓越周期T₁=4H/V_S2のときに式を変形してH= V_S2・T／4となることから、これを１/４波長則と呼びます。