岩級区分の新しい方法

Advertisements

比抵抗及び弾性速度分布の2種類の物理探査結果を合成することで、新たな地盤評価ができないか？という方針のもとで、研究した成果です。
これまでは、電気探査や電磁探査の成果の比抵抗分布と弾性波探査の成果の速度分布は、それぞれ別々に地盤評価をしていました。同じ地盤なのに？って思いで色々と試行錯誤した結果をまとめました。

1．まえがき

　トンネル地山の地質調査法に近年、物理探査法がよく用いられるようになり、従来の弾性波探査法に併せて電気・電磁探査法による比抵抗探査法もよく採用されている。現在、比抵抗を岩盤物性値としてとらえ、これによって、比抵抗の急変部を検出し、断層•破砕帯や地下水ゾーンの判定を行う試みが報告されつつあるが、まだ一定の解釈法が確立されていないのが現状である。また、山岳トンネルの調査では、弾性波探査や電気探査等の物理探査を行ってトンネル設計に反映しているが、その結果は別々に用いられているに過ぎない。

　筆者らは、MT法や電気探査法によって得られた地山の2次元比抵抗分布結果と、これに弾性波探査結果を併せて変換し、地山の間隙率分布や飽和率分布をもとめ、さらに、地山の岩級区分を2次元断面的に表示する一連の手法を検討した。そして、S地点の導水路トンネル工事掘削中における切羽観察資料を用い、本算定手法の検証を行った。

2.変換式による算定の概要

弾性波速度と比抵抗とは異なる物理量ではあるが、Wyllie(1956)の公式(1)式や、Archie(1941)の式(2)式

など、岩盤の間隙率や飽和率をパラメータとして関係付けることができる。

(1)式と(2)式とはφ,Sをパラメータとみれば、ひとつの岩盤要素について連立的に関係づけられるはずである。

(2)式については、修正を加え岩盤の比抵抗を空隙,間隙水,岩実質部に分解した、次のモデルを採用するものとした。

Advertisements

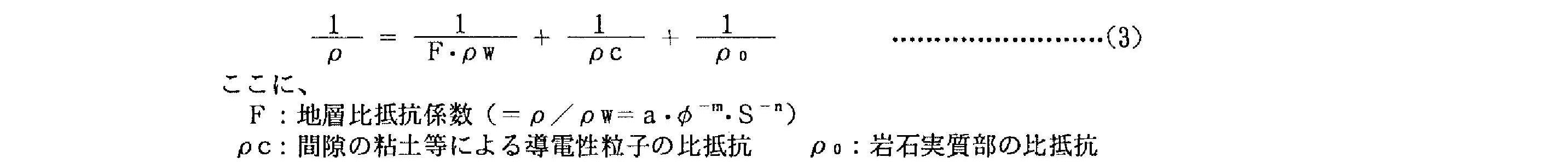
(1)式と(3)式とはφとSとをパラメ一夕にとれば、ひとつの岩盤要素についてそれぞれ次の関数関係に書き換えられる。

Vp＝ｆ(φ,S) ･････(4)　　　　ρ＝ｇ(φ,S) ･････(5)　

いま、要素について弾性波速度Vpと比抵抗ρとが与えられれば、(4)式と (5)式とを満足するひと組のφ,Sとが逆解析で求められる。従って、弾性波速度と比抵抗とが既知の地山について各要素ごとにVpとρからφ, Sを求め、さらに算出された間隙率φから岩級区分を推定することができる。
以上の作業手順をフローとして表すと図-1のとおりである。
なお、φ, Sを求める際にVpとρのどちらを重視するかを考え、重み係数α,βを導入した。

3.算定手法の検証

3-1 算定方法

算定手法を検証するため、S地点の導水路トンネル卜エ事における弾性波探査(図-2)及びCSAMT法による2次元比抵抗探査デ-夕(図-3)を逆解析により、間隙率分布及び飽和率分布に変換した。
当域の地質は、古第三紀の流紋岩類にひん岩•輝緑岩などの岩脈が小規模に貫入している。また、地表踏査とボ－リング調査の結果から風化が深部まで進み、破砕帯を伴う弱層もいくつか見られる。検証は地山の岩に対する岩級区分と間隙率との実測値がないため、表-1に示す関係を用いて間隙率から地山の岩鈒区分の分布図を計算し、これと掘削実績の岩級区分と対比して整合性をみることとした。

3-2 諸係数の設定

間隙水の比抵抗ρwは、地山の湧水地点における電気伝導率測定結果より、平均値の50Ω･mとした。
また、導電性粒子の比抵抗ρcについては研究文献3)とS地点のボーリングコアの比抵抗測定結果とから3,000Ω･mを仮定した。
岩実質部の比抵抗ρ0については、コアの自然乾燥状態における比抵抗測定値を参考に10,000Ω･mを適用した。
コ了の弾性波速度Vmは、同じくコアのVp測定値より6.5km/secを設定した。

次に、地層比抵抗係数Fに関する係数4)5)のａやｍ及びｎについては、変換結果の整合性をみながら想定される範囲内について種々の組合せに対し計算したが、S地点としては次の係数の組合せが良好であった。

　・ａ＝0.001
　・ｍ＝2.2
　・ｎ＝2.5
　・Ｖｐの重み係数α＝0.5
　・ρの重み係数β＝0.5

3-3 検証結果
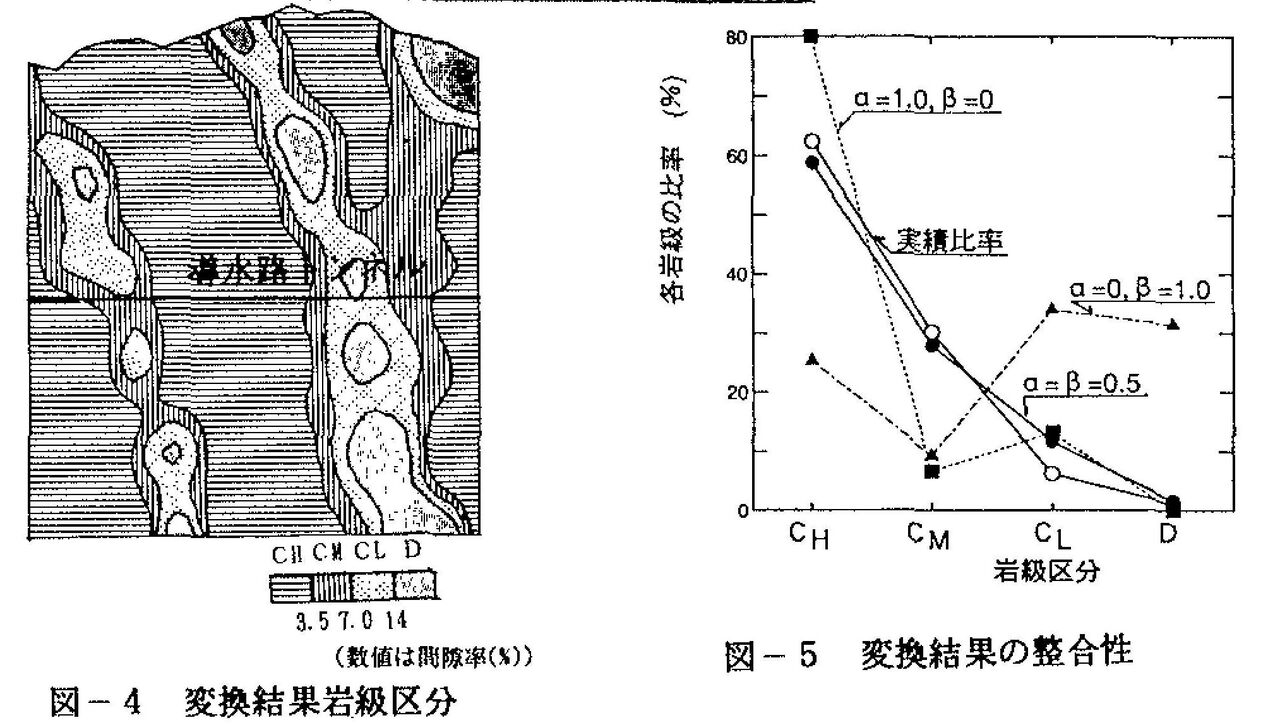
変換した検証区間の岩級区分の2次元断面図を図－4に示す。また、図－5はトンネル軸状のでの実績比率と変換結果の整合性を見たものである。図中には参考として、（α＝0，β＝1.0）と（α＝1.0，β＝0）とした場合も示すが、重み係数αとβの組み合わせは、種々計算したが今のところα＝β＝0.5程度が最も良い整合性を示した。

あなたも好きかも: