Advertisements
向一副摩擦副注入具有一定粘度的液體,摩擦副在相對運動的同時,液體會形成緊緻的薄膜,形成的壓力與外加載荷相平衡。情況完美時,流體形成的薄膜會把摩擦副兩個表面完全隔離,摩擦副之間的相對運動把粘性液體裹挾進收斂的間隙並產生動壓力,這就是流體動壓潤滑狀態。流體動壓潤滑問題的解決是建立在粘性流體力學理論上的,目前流體動壓潤滑理論大範圍地用在滑動軸承這些面接觸零件的設計上。
在19世紀末20世紀初,受限於科技水平,流體動壓潤滑被視為一維問題來分析,產生了無限長軸承理論,認為液膜壓力順著軸承長度方向幾乎沒有變化,液膜厚度方向同樣也幾乎沒有壓力變化,軸承圓周方向的壓力變化著重得到了研究。針對這個簡單的一維問題,得到的結論還是比較準確的,有力的推進了流體動壓潤滑理論的前進。人類邁入IT時代後,數值計算實現了高速化、大數量級化,二維以及三維雷諾方程的精確快速計算也進入了快車道。
解雷諾方程時,理論上應當先算液膜變形,然後就可以得到壓力分佈和其它參數。然而算變形卻需要先已知壓力分佈,這時候突然發現需採用迭代方法才能獲得數值計算結果。迭代時採取不同的算法,結果大相徑庭。
由數學角度來看,流體潤滑特性的研究過程等同於求解N-S方程或者雷諾方程,以便弄清流體中液膜壓力的分佈。考慮等溫條件,便忽略了潤滑液體的粘度和密度的溫度相關性。除此之外,雷諾方程推導中還需要以下幾個假設:
(1) 不考慮體積力的作用,如重力或磁力。在一般的流體狀態下,這個假設都是合理的。
(2)流體緊緊地依附於固定界面上,並無相對位移。
(3)忽略液膜厚度方向上的壓力變化。在微米量級,忽略沿液膜厚度的壓力比那話,這時粘度以及密度也不隨厚度方向而變化。
(4)與微米量級的液膜厚度相比,摩擦副表面的曲率半徑數量級較大,由此不必考慮曲率引起的速度方向的改變。
(5)牛頓流體的定義適用於潤滑液體。
(6)流動為層流,不存在渦流和湍流。
(7)對比粘性力,可以不考慮慣性力的作用,包括液體加速的慣性力以及液膜彎曲的離心力。
經過推導可得到雷諾方程的表達式:
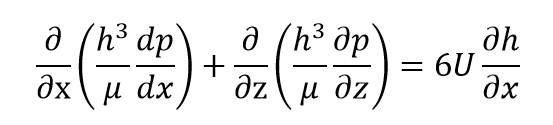
其中μ為液體動力粘度,U為轉子的運動速度,p為液膜壓力,h為液膜厚度。
軸承在艇體某種確定工況下工作時,若能使潤滑膜厚度減少單位長度,需要潤滑膜增加一定的載荷,這個載荷值就是滑動軸承的液膜剛度。當外載荷加到某個值時,液膜再也不能支撐而發生大量破裂,此時的極限載荷就是軸承的承載能力。軸承的剛度矩陣和阻尼矩陣統稱為液膜動力特性矩陣。宋強經過研究發現,當軸承的形式、尺寸、載荷、潤滑油條件確定時,油膜動力特性矩陣僅取決於軸的轉速。

