採用ANSYS中的Fluent模塊對推力軸承的動特性進行分析。在分析之前,需要用繪圖軟件得出軸承的液膜剛度幾何模型,然後對幾何模型進行預處理。
可傾瓦軸承潤滑膜幾何模型的建立
採用SOLIDEWORKS三維繪圖軟件對可傾瓦軸承油膜進行建模。在此之前,需要明確幾個參數。對於扇形可傾瓦軸承的間隙比c,可以採用下面的公式進行計算:
d_l/d=(c(c+2)lnc-(c-1)(2.5c+0.5))/((c^2-1)lnc-2(c-1)^2 )
其中,d為軸瓦上面出油口與進油口之間的長度,d_l為瓦塊上固定支點與進油口之間的長度, dl/d是支點位置,衡量了支點在瓦塊上的相對位置。依據本文實例,dl/d =0.5。經過簡單的計算可以得到間隙比c=2.36。
推力軸承共有8塊扇形瓦塊,某個扇形角均是40度,扇形瓦塊之間的角度為5度。扇形瓦塊靠近軸的一端所形成的圓的半徑r=86.5mm,瓦塊遠離軸的一端形成的圓的半徑R=182.5mm,各個扇形瓦塊之間間隙處軸向液膜厚度e=10mm ,支點位於瓦塊面中心。
採用SOLIDEWORKS作為繪圖軟體,進行可傾瓦推力軸承油膜的三維幾何建模。為了方便對幾何模型的預處理,在繪製可傾瓦軸承油膜幾何模型時將兩塊扇形瓦之間的間隙分成平均兩份,與單個瓦塊一起建模。
可傾瓦軸承潤滑膜幾何模型的預處理
將建立好的幾何模型接入ANSYS中的ICEM CFD模塊,把‘單位’一欄改為毫米。在'PARTS'層面將幾何模型做出分割,中下端的弧形表面定義為'入口',上端的弧形表面定義為'出口',底端的表面定義為'旋轉軸',扇形瓦面和軸接觸面都定義為'牆壁'。幾何模型左側以及右側的表面定義為P1、P2。在‘整體網格’設置中,找到“週期”,設置旋轉軸為Z軸旋轉45°。這樣就可以把單個油膜模型擴展為完整的8個。
所分析推力軸承採用油潤滑,故選取材料庫中的fuel-oil-liquid,密度為0.96×〖10〗^(-3) Kg/m3,動力粘度為0.048Pa·s,轉速為40rad/s,特徵長度為1×〖10〗^(-4) m。由於Re=13.8<2100,為層流狀態。採用六面體網格型式對幾何模型進行網格剖分,在創建塊時,要確保能夠完整囊括幾何模型。把旋轉重合面進行關聯,在“編輯塊”選項卡中編輯“週期頂點”。結合幾何模型的特點,對塊進行處理,盡量接近初步幾何模型的形狀,最後把線進行關聯,調節各個節點以獲得更好的預處理效果。全面關聯之後,對各種尺寸進行調節,適當把軸瓦之間流體部分的網格做的稀疏一些,這樣可以提高運算速度。綜合考慮運算精度和速度,當所劃分的網格數量達到1.5×〖10〗^5時就可以進行下一步分析運算了。下圖為經過預處理的一個油膜扇面。
Advertisements

至此,就創建了推力軸承潤滑膜的幾何模型,並進行了網格剖分的預處理。在這個基礎上,就可以把預處理結果導入到Fluent模塊,然後根據實際情況,設置好相應的條件,進行分析,進而得到不同轉速之下的可傾瓦推力軸承的油膜剛度值。
利用FLUENT模塊對可傾瓦推力軸承進行動特性分析
對推力軸承做具體的動特性分析。首先將預處理結果接入到FLUENT模塊,選用Double精度級別的壓力基運算模塊進行液體的動特性運算。對網絡剖分情況檢查完畢後,採用恰當的縮放比例,把毫米定義為全局的單位,採用Laminar模型。鑑於可傾瓦扇形推力軸承的特殊結構,軸承工作時並不會產生負壓,油膜不會破裂,故這裡不需要引入空穴模型。對於流體材料,選取fuel-oil-liquid,把進油處及出油處的壓力定義為5×〖10〗^4 Pa。
扇形的推力瓦塊形成一個圓盤,沿著軸向,分佈在推進軸階梯的前面與後面。根據可傾瓦推力軸承的尺寸,單側的扇形瓦油膜標準間隙為0.1 mm。記前面推力盤與階梯的間隙為J_q,後面推力盤與階梯之間的間隙為J_h,容易知道,存在這樣的關係:J_q+J_h=0.2mm。分別設置一系列的推力軸轉速,並將J_q(或者J_h,最終結果是一樣的)設置為0.03mm-0.17mm的一系列數值,經過FLUENT仿真計算,可以得到在不同預定軸轉速情況下,J_q與軸承總推力的對應關係。
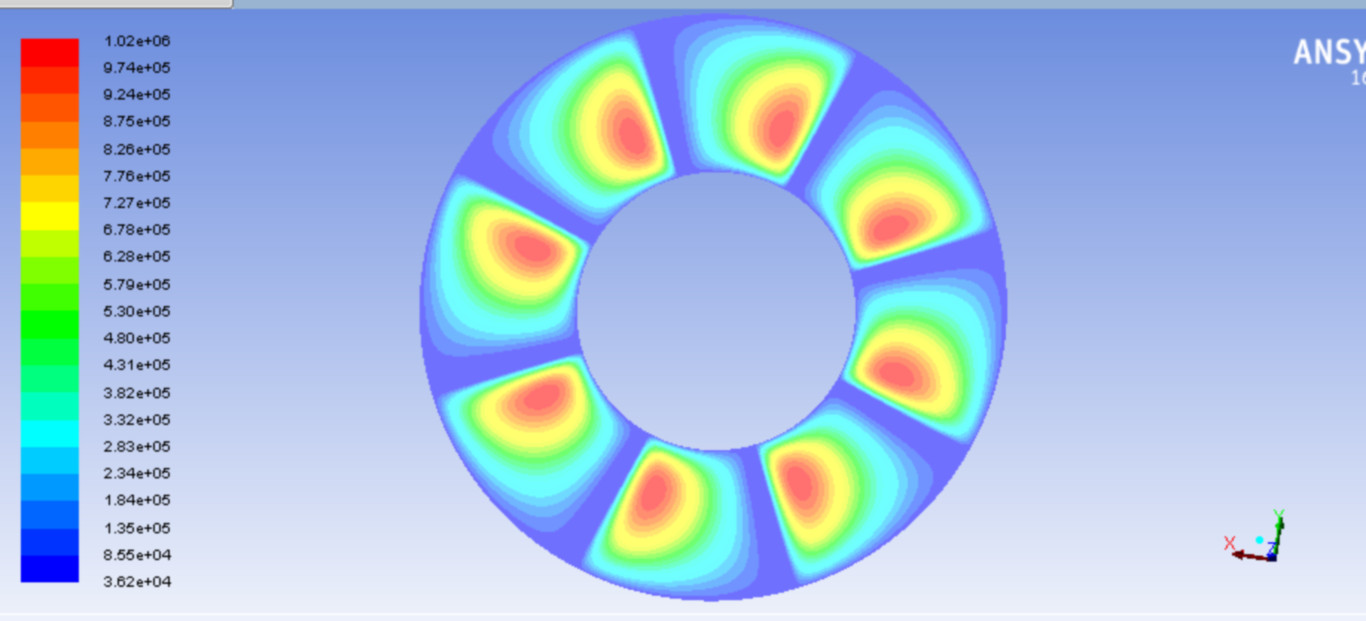
當限定推力軸轉速和J_q為某一定值時,可以得到該狀態下整個扇形潤滑區域所組成的圓盤潤滑膜承載力分佈圖。為了更加清晰的查看某一工況下可傾瓦推力軸承的油膜承載力分佈,分別取轉速為15rad/s,單側油膜間隙J_q=0.06mm,得到瞭如圖所示的承載力雲圖。顏色越接近紅色,表示潤滑膜的提供的壓力越大。從圖中可以看到,緊捱的兩塊扇形瓦塊之間的矩形區域內油膜壓力很小,沒有為軸承提供主要的軸向推力。這反過來佐證了對於這一區域進行稀疏網格剖分的合理性。對這一矩形區域進行稀疏的網格佈局,而對扇形區域進行較為密集的網格劃分,這樣既保證的整體運算的精度,也提高了運算速度。
Advertisements
把得到的數據轉化為散點圖,並做近似線性化處理,可以得到可傾瓦軸承潤滑膜承載力-間隙-轉速關係圖,如圖所示的。五條直線分別表徵了不同工況(表現為推力軸轉速不同)之下潤滑膜承載力與推力軸承-軸單側間隙J_q的關係。當間隙由大變小時,潤滑膜受到的壓力逐漸加大,這與流體動力學中關於流體承載力的描述相一致。同時注意到:推力軸轉速較高時,油膜承載力-軸承間隙之間的線性關係不明顯,在推力軸轉速低的範圍內,線性關係則較為明顯。轉速提高後,整個軸系的振動形式都更加複雜,而在低速區域,則有跡可循。
根據軸承潤滑膜剛度的定義,對圖中的各個曲線所對應的直線方程求導數,可以得到不同轉速之下的可傾瓦推力軸承潤滑膜剛度。將剛度的單位換算為N/m,得到了不同工況之下的位於軸系中段的可傾瓦扇形推力軸承的潤滑膜剛度值K_L。最終得出的剛度數據與相關文獻上面的數量級十分吻合,證明計算結果是有效的。


