徑向軸承剛度特性分析

艉前、艉中、艉後三個徑向滑動軸承在結構上類似、潤滑原理相同，具體的尺寸有所差別。在計算液膜剛度時，方法完全一樣。所以首先以艉前軸承的計算為例，進行軸承剛度分析。

潤滑膜幾何模型建立及預處理

為了進行艉前軸承液膜剛度的分析，需要首先做幾何建模和預處理。需要對實際軸承的參數進行一些處理，用於參與計算。

對於艉前軸承的潤滑液體的幾何模型的建立，依然採用軟件Solideworks為繪圖工具，按照給定的尺寸，可以得出艉前軸承液膜分佈的幾何模型。

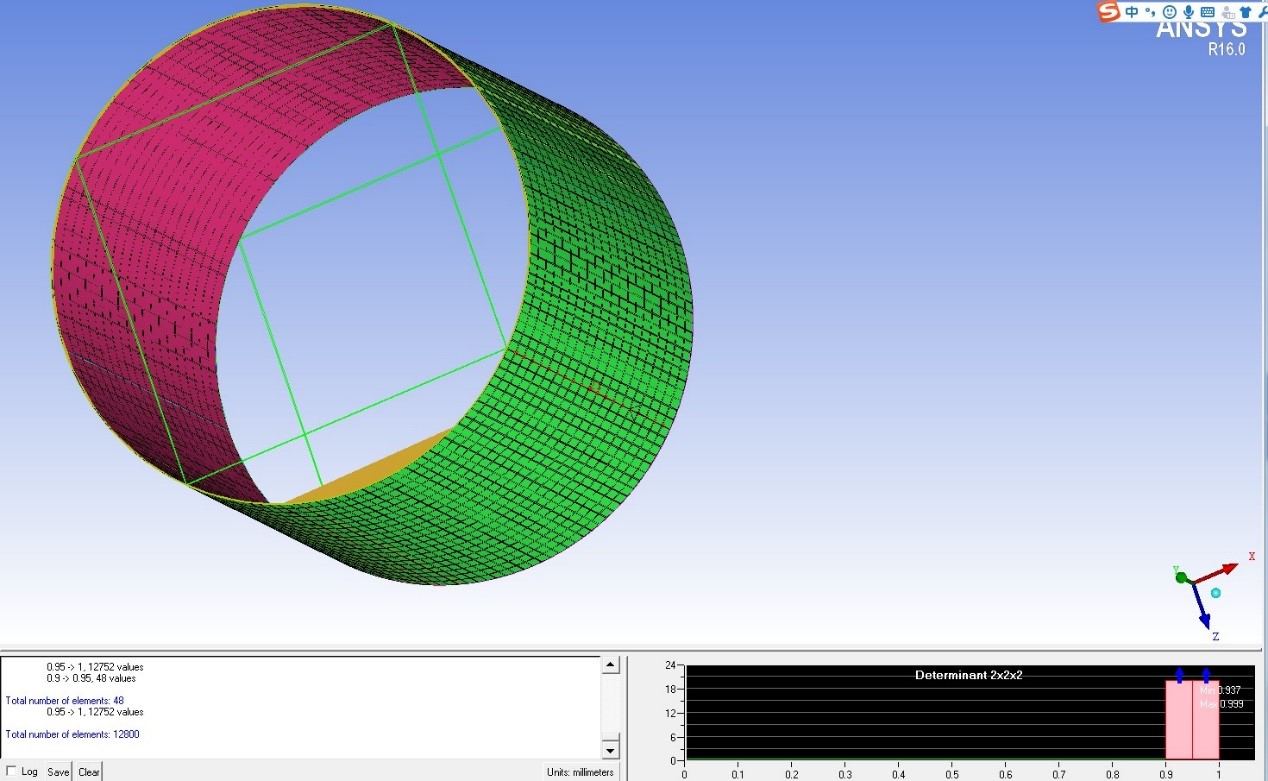
在將初步建立的幾何模型導入到ANSYS之前，需要對幾何模型進行一些處理，以便於和ANSYS中的ICEM CFD模塊相互適應。對幾何模型的預處理，以六面體作為劃網格的基本單元。在劃分過程中，需要綜合考慮液膜厚度、寬度、流動狀態等因素。

在對幾何模型做劃分網格的操作時，細小的網格形式可以提高後期計算的精確度，但同時會加大計算機的負擔，拉長計算週期；相反的，採用較大的網格形式可以顯著加快計算時間，但是會降低計算精確度，甚至出現較大的誤差。為了獲得最優的結果，需要綜合考慮運算的精度以及計算機的實際情況，做出最合理的幾何模型的網格剖分方案。

在幾何模型導入ANSYS之前，注意查看整體的尺寸單位是否為mm，確定之後，將處理後的幾何模型導入到ICEM CFD之中。建立parts，把任意一個圓環端面設定為入口，另一端即是出口，外側圓柱面為wall，內測柱面設為axis。

徑向滑動軸承潤滑膜的剛度特性分析

按照滑動軸承液膜剛度的定義，只需對潤滑膜設定徑向的一個偏移，用FLUENT分析相應的壓力就可以得到潤滑膜的徑向剛度。給定轉軸的偏心率由0.1逐步增加到0.6，步長為0.1，對應的偏心距就會從以步長0.01由0.01增加到0.06。

先以艉前軸承為例，進行徑向滑動軸承的剛度分析計算。然後，按照同樣的方法，得出其餘兩個徑向軸承的液膜剛度值。

回顧徑向滑動軸承潤滑機理，潤滑膜在最小厚度之後某一處發生破裂，在微觀上會表現為產生氣穴。此處流體由液體的單一形式，變為氣-液的雙相形態。如果在運算中不引入氣穴模型，由於超薄潤滑膜附近的負壓區，後期通過壓強分佈計算受力時發生較大誤差。考慮到這個情況後，意識到有必要在液膜壓力分佈的分析計算中引入氣穴模型。

Advertisements

打開Fluent軟件，將預處理完成的幾何模型導入其中。解算器方面，採用Double精度級別的三維度壓力基解算器。將UNITS設定為mm。此處採用Laminar這一層流的流體模型。氣穴模型這塊，選用fuel-oil-liquid和fuel-oil-vapor。在界線狀態欄定義邊界條件，進口為壓力入口，出口為壓力出口，壓力都定義為5×〖10〗^4帕斯卡。軸轉速按照5-25rad/s，步長為5rad，選取4個取值，此外為了模擬真實航行工況，增加40rad/s的軸轉速，進行計算。針對前述的氣液雙相的情況，為了減少計算誤差，這裡決定採用Singhal-et-al模型。

在model中，選擇混合模型，這種模型有兩種相。依次輸入solve-回車-set-回車-expert-回車-no。詢問是否使用Singhal-et-al，鍵入“yes”並回車。

選好這種模型後，就要對雙相模型的基礎相和從屬相進行一些整理，通過菜單欄裡的“定義-相”進行調整。在Interaction中設置模型狀態為中空狀態，在質量中把7750帕斯卡作為氣穴的壓力值鍵入其中。這樣的設定目的是，潤滑液壓力低於它時會發生氣-液的形態轉化，此時表面張力係數達到0.0717 N/m。

設定不同的偏離率ε，與這個偏心方向相同的方向的受力定義為F_y，與F_y垂直的分力定義為F_x，F_合為它們的合力，F_x與合力之間的夾角為α ，偏心率ε在合力方向的投影長度為L_OA。圖4-4展示了偏心率ε、夾角α與合力方向投影的關係。即有L_OA=ε·sinα，只要將仿真得到一系列的F_x和F_y進行矢量求和，就可以得到F_合，相應的液膜剛度即為

k=F_合/L_OA =F_合/(ε·sinα)

其中，tan⁡α=F_y/F_x 。

在使用軟件進行仿真計算時，設定步長是1000，達到收斂條件時就會停止計算並返回結果。給定一系列的偏心率，得到不同轉速之下的F_x和F_y。具體的仿真數值結果。

根據幾何關係，對數據進行處理，可以得到合力F_合與合力方向的偏移量L_OA之間的函數關係。

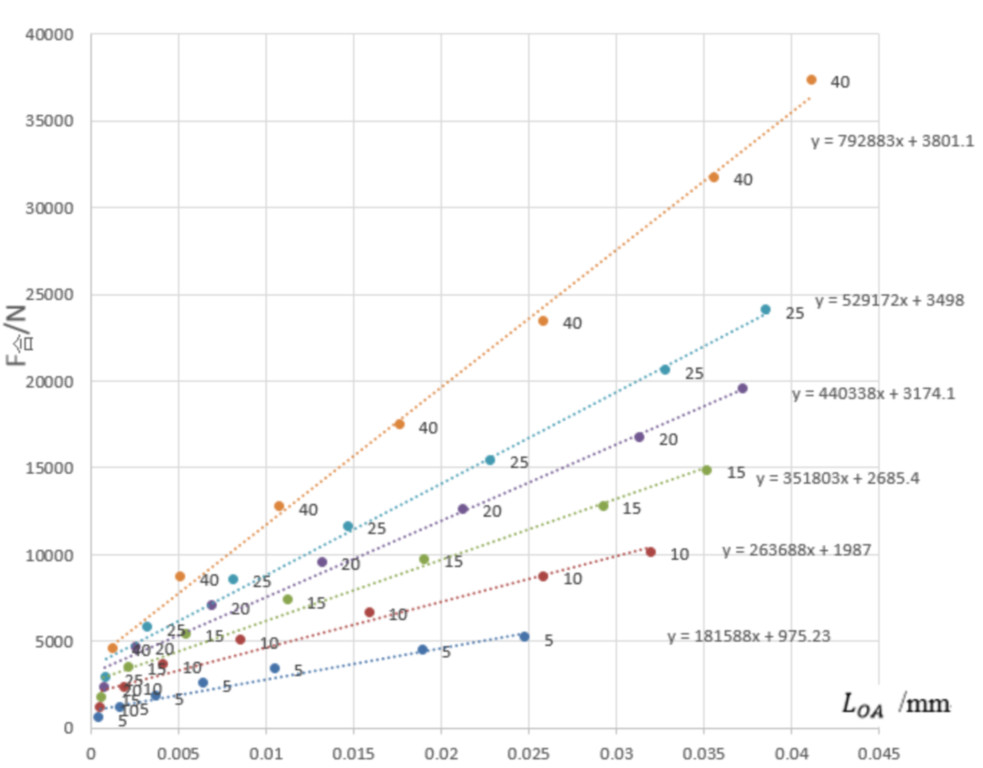
為了考察所展示的函數關係，可以把L_OA-F_合的相關點，呈現到一個直角坐標系中。經過曲線擬合，發現它們呈現較好的線性，那麼對應直線方程的斜率就是轉速為5rad/s時的液膜剛度值。把轉速為5、10、15、20、25、40rad/s對應的函數關係全部列到一個坐標系中，得到不同工況的偏移-合力圖。