Advertisements
推進軸系尾段的軸段上,依次分佈著推力軸承、艉前軸承、艉中軸承和艉後軸承。
推力軸承為可傾瓦扇形瓦塊油潤滑軸承,艉前、艉中、艉後軸承為徑向滑動水潤滑軸承。徑向軸承主要起到徑向的約束,對於沿著軸的方向的振動能量傳遞關係不大。與徑向軸承不同,推力軸承由於自身的結構與潤滑特點,它的縱向剛度對於軸系的縱向振動具有較大的影響。探討幾個滑動軸承的動特性與軸系縱向振動之間的影響規律,主要就是考察在不同螺旋槳軸的轉速之下,可傾瓦推力軸承油膜剛度產生不同的變化,進而對於軸系縱向振動能量的傳遞發生了一定的聯繫與影響。
此外,分析艇體航行時這幾個滑動軸承的動特性規律,主要是對軸承的液膜剛度和阻尼進行分析。而考慮到軸承的液膜剛度對於軸系-艇體系統振動能量傳遞的作用更大,這裡僅僅分析各個軸承尤其是推力軸承在不同軸的轉速下的液膜剛度變化情況對於軸系縱向振動能量傳遞的影響。此前已經對可傾瓦推力軸承的液膜剛度進行了詳細的計算。在這個基礎上,將對軸系縱向振動的動力學模型進行修正,列寫並求解微分方程。
對船艇推進軸系的縱向振動進行分析時,有很多方法可以選擇。例如霍爾澤法、四端參數法和有限元分析法。四端參數法又叫傳遞矩陣法,它可以改變研究對象微分方程的計算模式,把複雜的微分積分計算轉換為簡單的矩陣計算,這對於較為冗雜研究體系的分析計算至關重要。
漿-軸-推力軸承-艇體縱向振動能量傳遞的簡單分析
首先對軸系分段建立動力學數學模型,然後就可以用傳遞矩陣法進行求解分析。
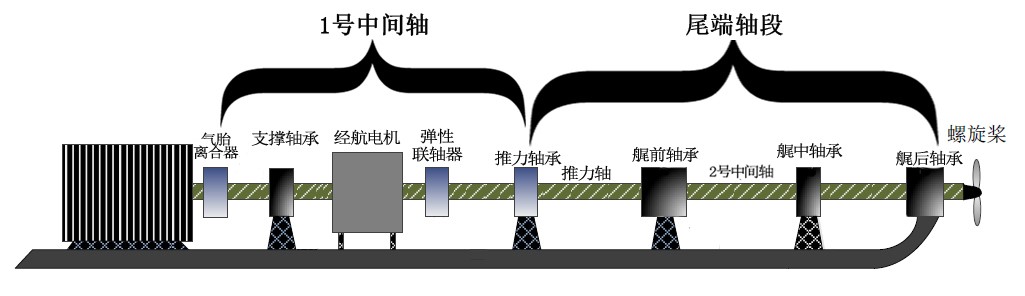
為了便於下面的分析,將氣胎離合器到可傾瓦推力軸承的軸端稱為1號中間軸;把其餘的軸段稱為尾段軸段。在推進軸系的最前端,是主推進電機,最末端是由槳葉組成的推進器。電機的源動力通過中間的軸系和各種部件傳遞到尾端的槳葉,槳葉攪動海水,推動船艇前進。受限於自身結構,在航行時槳葉周圍會產生不均勻的伴流場,這導致從槳葉傳遞到軸系上的推力也產生不均衡的周期激勵,這導致了軸系的縱向振動。從槳葉傳遞而來的推力通過可傾瓦推力軸承傳遞到艇體,而推力軸承的整體剛度偏“硬”,故尾端軸段的力與功率流的傳遞規律應當是本章優先分析計算的部分。與此相對應,靠近主推電機的離合器的縱向剛度較為“軟”,對縱向振動傳遞的影響較小,所以這裡不再分析1號中間軸上面的縱向振動能量的傳遞規律。
建立軸系縱向振動動力學模型時,有一些假設和前提:將螺旋槳看作是只有質量,幾何形態為一個點的剛體,推力軸承的油膜剛度則參考此前的計算結果。
Advertisements
漿-軸-推力軸承-艇體縱向振動動力學方程的推導
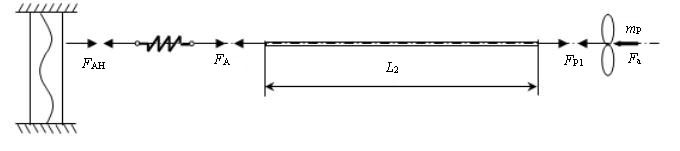
圖給出了尾段軸段的力與能量的傳遞示意圖。圖中,L2為尾段軸段的長度,mp為螺旋槳質量,Fa為螺旋槳激勵,FP1為位於軸內部的螺旋槳與軸之間的縱向推力,FA為可傾瓦軸承與推進軸相連處的內部縱向激振力,FAH為由可傾瓦軸承油膜傳遞到軸承座(艇體)上的激振力。
關注圖的最右側,以螺旋槳作為研究對象,它同時受到的力有周期推力力(F_a ) ̃和周期內力(F_P1 ) ̃。規定船艇前進方向為正方向,在圖中為向左。定義槳葉在各種週期力的作用下向左的交變移動量為,在不均衡伴流場中槳葉所在環境的阻尼係數為(C_P4 ) ̃。有如下的力學方程:
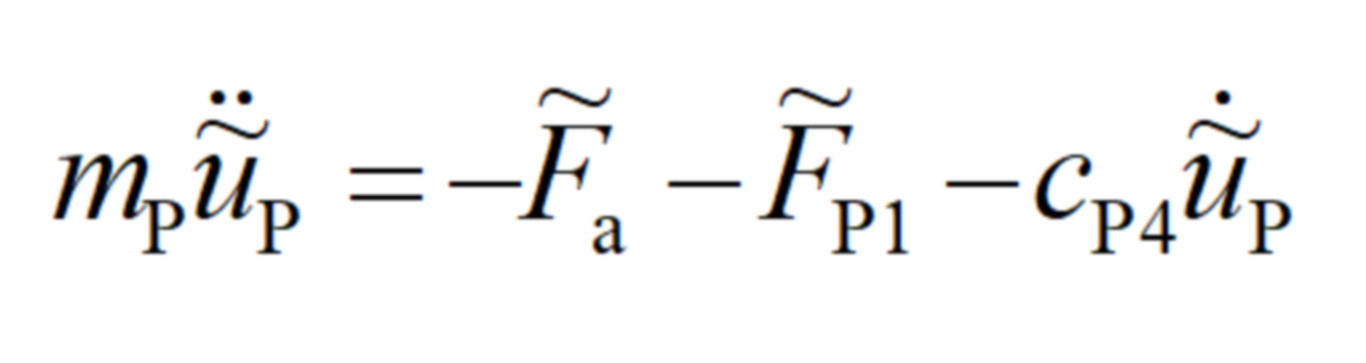
Advertisements
關注位於圖中間的軸段。該段軸在周期性的力(F_a ) ̃作用之下,沿著軸向產生週期性的位移,設在某處x_2(0≤x_2≤L_2)的移動量為,質量均勻分佈的軸密度為ρ_2,截面面積為S_2,彈性模量為E_2,可以得到中間軸段的動力學方程。
接下來考察可傾瓦軸承的受力情況。根據以前的計算結果,在轉速較低的範圍內,軸承油膜的剛度特性表現為較規律的線性,設油膜剛度為K_A。根據胡克定律,油膜的周期承載力為:
(F_A ) ̃=k_A δu=(F_AH ) ̃=k_A ((u_LR ) ̃-(u_LL ) ̃)
其中,(F_AH ) ̃是通過可傾瓦軸承油膜傳遞到軸承座及艇體的周期力,(u_LR ) ̃是軸承與艇體相結合處的振動位移。
在圖中,槳葉處產生週期性的激振力,依次通過尾端軸段、可傾瓦推力軸承、軸承座、軸承座與艇體連接處,最終傳導到艇體之上。對軸承座-艇體連接處進行模態分析,把位移(u_LR ) ̃用振型的疊加模式表達出來。
對漿橫向激勵作用在尾端軸段,產生噪聲輻射的情形進行了分析,分段對槳、尾段軸、軸承、軸承座與艇殼體進行了動力學分析,得到了縱向方向的軸系振動動力學模型。為下一步對軸系的縱向振動情況進行功率流分析做好了準備工作。