為了運用功率流分析的工具對振動能量在沿著軸向方向的傳遞規律，需要對各個動力學方程進行求解。對其中的各個方程進行傅立葉變換，可以將動力學方程簡化。可以化為
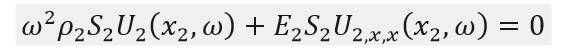
Advertisements
用 代表波數，並且
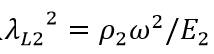
它的通解可以表示為
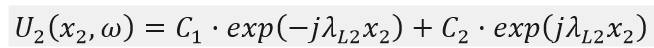經過計算，可以得出通解中的係數：
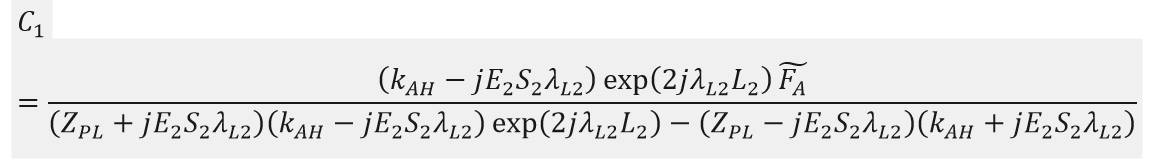其中，存在以下關係：
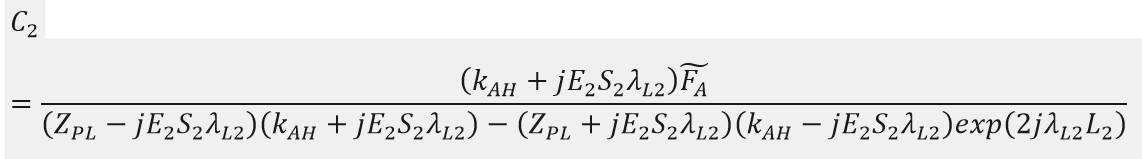
求解以上方程，可以令
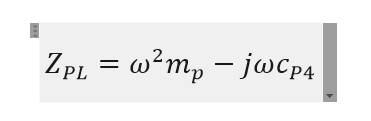
滿足這個超越方程的都是解，也即振動的固有頻率。顯然有無窮多個 滿足這個條件。
搞清楚槳-軸-軸承-艇體複雜縱向振動傳遞動力學方程的求解之後，下一步就是運用功率流方法對縱向振動的各個環節進行功率流分析。
簡諧激勵情況下，功率流的一般表達形式是 。採用這種方法對某個模型進行振動分析，有以下優點：同時考慮傳遞在某一結構上，力和速度兩個度量維度；功率流提供了針對振動能量傳遞的唯一絕對度量，這個度量值可以通過儀器直觀的衡量出來；
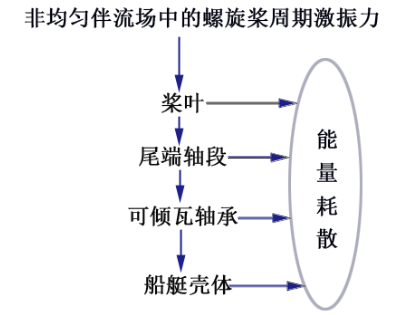
通過數值求解，分析可傾瓦推力軸承的油膜剛度特性與縱向振動之間的一些聯繫。振動能量從最初源自槳葉處的周期性激振力，歷經各個環節傳遞耗散後到達艇體，下圖示意表達了這一過程。
槳葉處的周期激振力 經過一系列傳遞，導入到軸系的振動能量是：
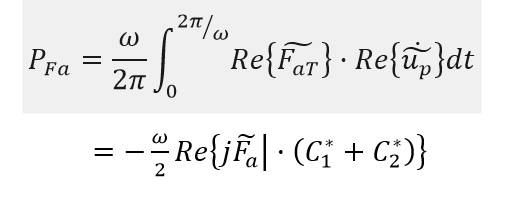
Advertisements
槳葉在航行中克服海水阻尼，產生振動能量的耗散，損失的平均功率是
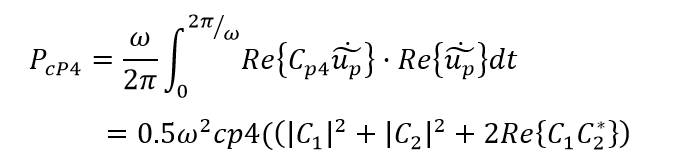
定義航行方向為正方向，槳轂處的功率流為
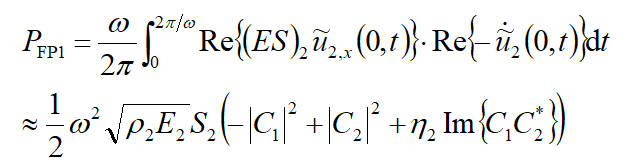
有復數形式
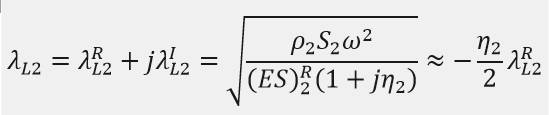
週期激振力經由可傾瓦推力軸承傳導到軸承座以及船艇殼體的功率流是
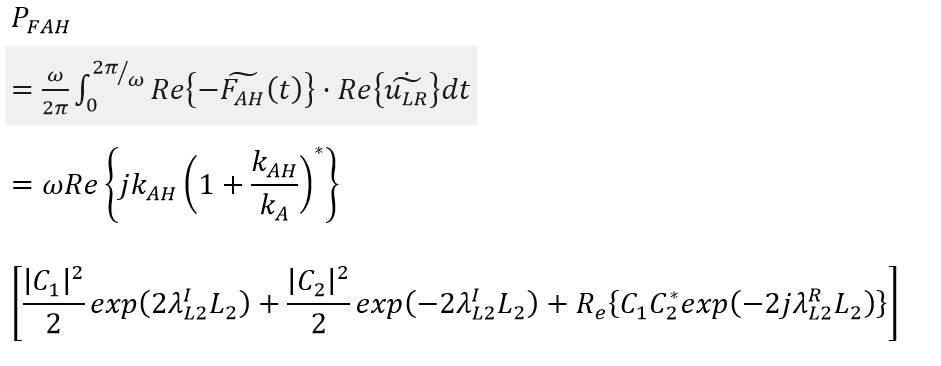
接下來，為了更加清晰的對振動能量在漿-軸-軸承-艇體中的各個環節的分佈與散發情況，分別導出各個部位的振動能量密度。
考察尾端軸段，沿著軸向的平均能量密度是
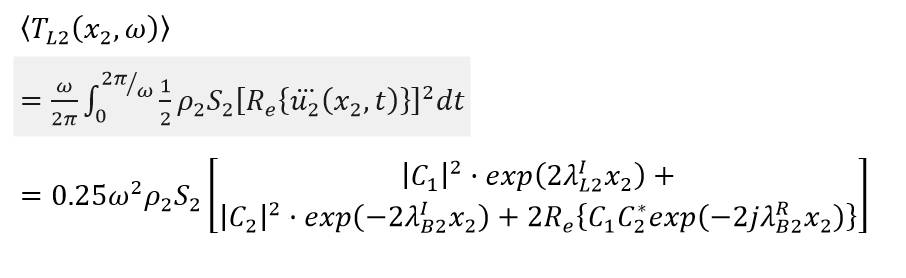尾端軸段的時間平均彎曲變形勢能密度是
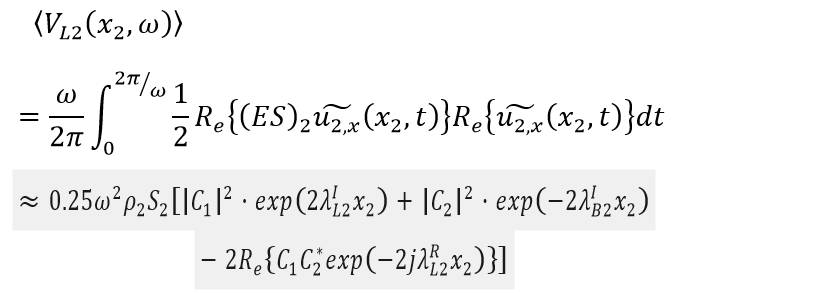
尾端軸的（時間平均）縱向振動能量密度：
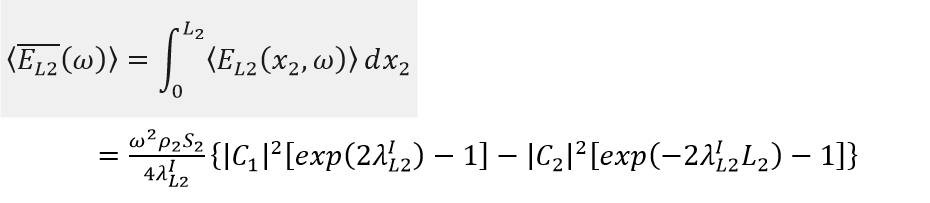
螺旋槳在縱向振動中的時間平均能量是
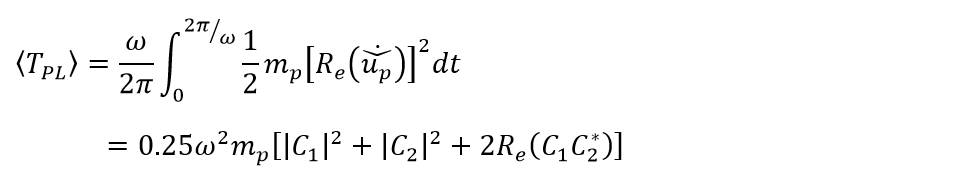
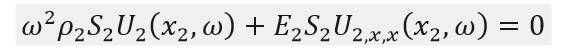
Advertisements