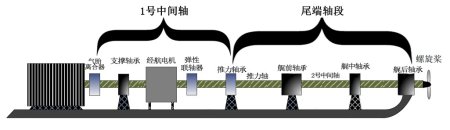
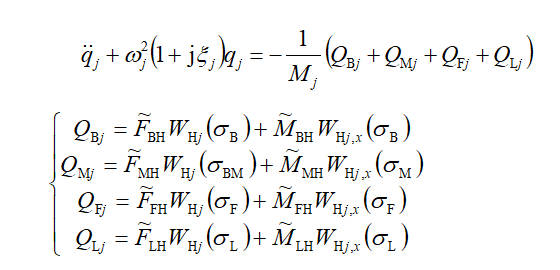在推進軸的末端,槳葉受到的垂直於推進軸方向的周期性激勵分量作用,傳導到軸上面,這是推進軸系產生彎曲振動的原因。其中,將軸視為梁,艉後軸承的徑向剛度約束極大,彈性聯軸器處的徑向約束和轉角約束較小。所以,忽略1號中間軸,而只考慮槳葉到聯軸器(推力軸承)之間的尾端軸段。
為了便於對軸系進行振動能量傳遞的動力學分析,把尾端軸段劃分為槳、螺旋槳軸(由螺旋槳到推力軸承的中間軸段)、各個支承(艉前、艉中、艉後軸承及其軸承座)、艇體幾個分部進行分別分析,隨後再進行功率流分析。為了更加便捷的進行研究,把四個軸承與艇體連接處視為點接觸、忽略軸承寬度。
Advertisements
從圖中可知,存在:

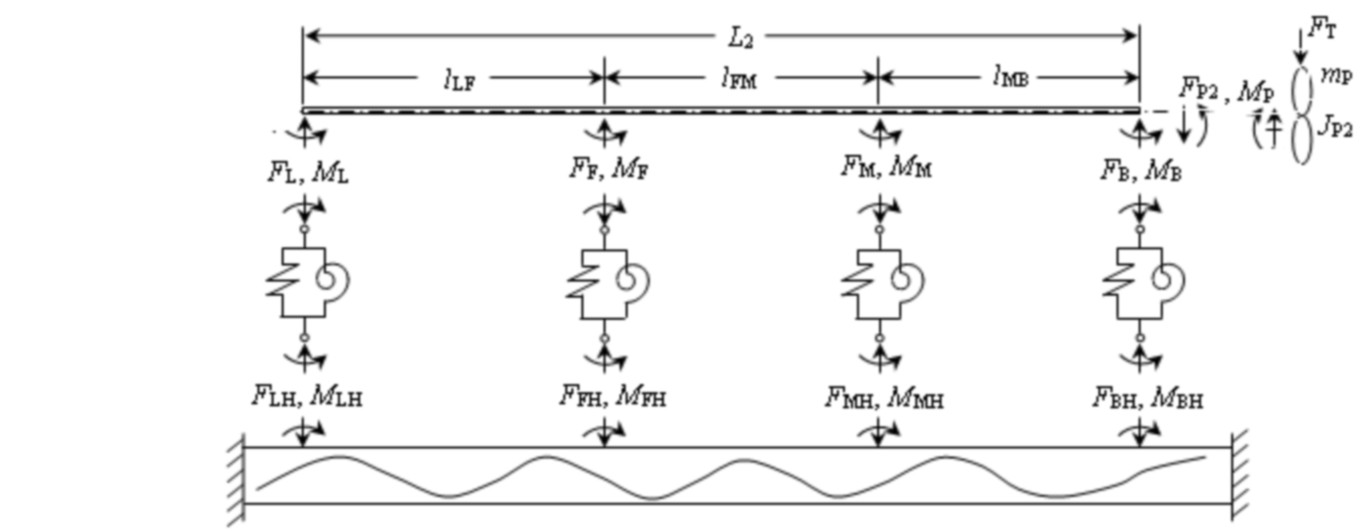
軸系彎曲振動運動學模型
在橫向激勵作用下,螺旋槳軸發生了彎曲振動。槳作為附加到軸尾端的剛體,受到週期性的交變螺旋槳力 作用的同時。此外,在軸與槳的接觸處,內在剪力 和彎矩 也作用到了螺旋槳上面。槳的質量為m_p,J_P2是順著彎矩M_P方向的轉動慣量,螺旋槳順著M_P方向的周向角度為 。設定豎直向上為正方向,以螺旋槳為研究對象,列寫動力學方程:
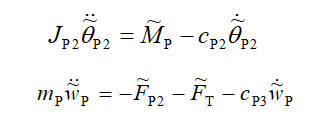
2號中間軸與推力軸共同組成了尾端軸段,上面有多個支撐點用來加強軸段的結構強度。在槳葉週期力作用下,彎曲的振動在這個軸段上產生了。在軸段的某一處,某一時刻的橫向振動移動量用來表示,這裡的橫截面積與密度、抗彎剛度分別用S2、 與(EI)2來表示,採用歐拉方程可以描畫彎曲振動情形:
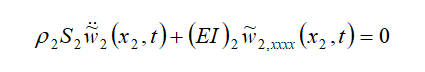
對於各個軸承之間的軸段,都可以用來描述其中的彎曲振動。為了便於分析,把軸承與軸的接觸視為點接觸,它們之間的作用關係看作集中的力和力矩的作用。如此得出了分為三段的函數關係:
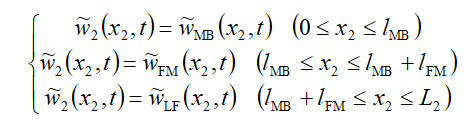
在軸段的兩端,約束條件是:
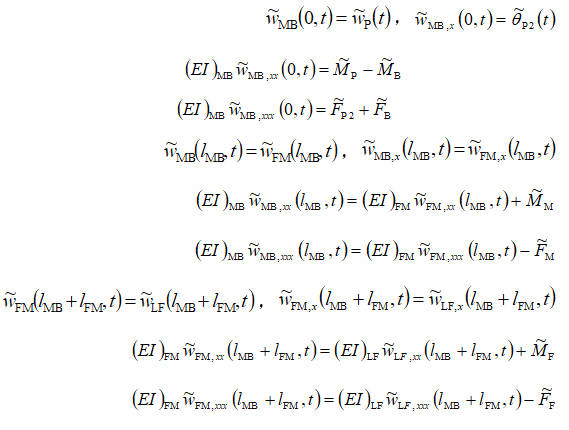
在尾段的推力軸上面,存在四個滑動軸承,其中三個是徑向軸承,一個是可傾瓦推力軸承。對通用的滑動軸承模型進行分析,轉子(推力軸)在彎曲振動作用下離開原平衡位置,設徑向位移為δs,偏離角為δθ,一部分潤滑液體受到壓迫,產生力δF和力矩δM,促使轉子向新的平衡位置移動。假設壓力和壓力力矩分別與相應的位移偏移和角度偏移成正比。
根據以上的設定,分別對四個軸承列寫動力學方程:
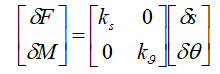
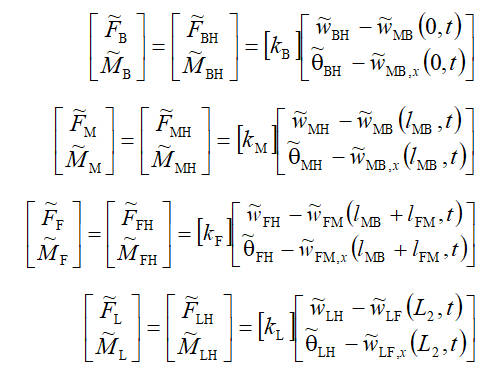
接下來,要對各個軸承的軸承座與艇體連接處進行分析。考察彎曲振動,振動能量經由軸承潤滑膜傳遞到軸承座,進一步傳遞到艇體殼,使其產生豎直方向的振動位移,用表示這個位移,位移響應點在艇體中的位置坐標用δ表示,艉後、艉中、艉前、推力軸承的軸連接處的位置坐標用B、M、F、L表示,那麼振型疊加態是(廣義坐標 ):